Présentation générale
Le 11 novembre 2019, le passage de la planète Mercure devant le Soleil pourra être observé et durera au maximum près de 5 h 28 min.
En France métropolitaine, le phénomène débutera à 13 h 35 min (heure locale française). Il ne sera pas visible dans sa totalité, car le Soleil se couchera avant que le passage ne soit terminé, mais pourra toutefois être observé jusque 17 h 20 min environ. La hauteur du Soleil demeurera constamment inférieure à 23°.
La carte ci-dessous donne les lieux de visibilité sur Terre.
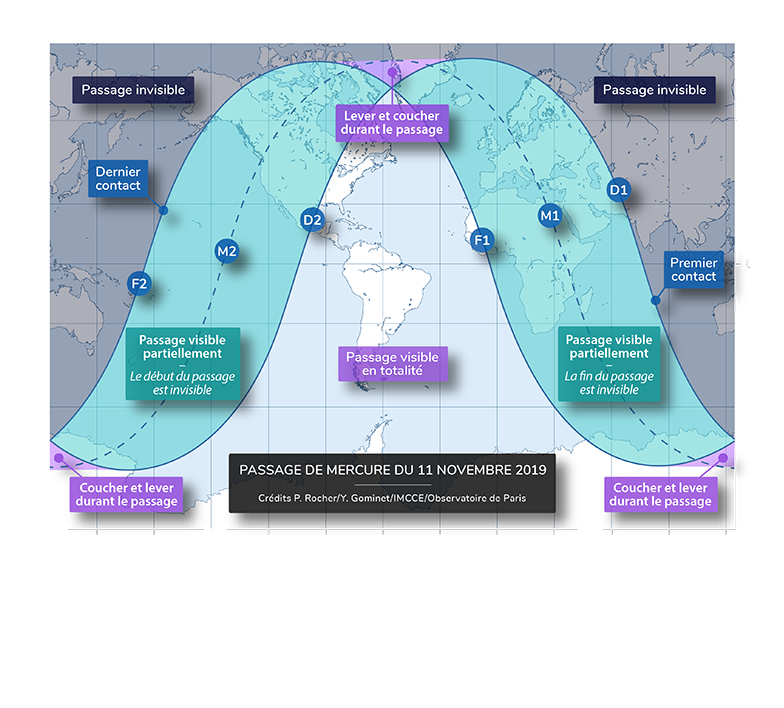
Sur la carte, les courbes représentent les limites de visibilité du passage de Mercure aux couchers et aux levers du Soleil, respectivement de droite à gauche. Tout lieu situé dans la région centrale permettra l’observation de la totalité du phénomène. Cette région comprend l’est de l’Amérique du Nord, l’Amérique du Sud, le sud du Groenland et l’extrème ouest de l’Afrique.
Afin de ne rien manquer du spectacle qui se prépare, ce portail de l’IMCCE vous propose un formulaire interactif qui vous permettra de calculer les circonstances locales de visibilité du passage de Mercure pour tout lieu sur Terre.
Il vous est également possible, au moyen d’un second formulaire, de rechercher la valeur de la parallaxe solaire en procédant à la mesure des différents instants de contact entre le disque de Mercure et le disque du Soleil.
Attention !L’observation directe du Soleil ne doit jamais être faite à l’œil nu sans protection : il est nécessaire de prendre les mêmes précautions que pour l’observation d’une éclipse de Soleil.
Il est ainsi recommandé de procéder par projection de l’image du Soleil sur un écran blanc. Un moyen simple et commode pour observer en toute sécurité est l’usage d’un petit instrument appelé « Solarscope » : le modèle éducation produit une image du Soleil de 122,6 mm de diamètre sur laquelle Mercure apparaîtra comme un minuscule disque de 0,63 mm de diamètre. Avec un tel instrument, le suivi de la « route » de Mercure sur le Soleil peut être effectué et donner lieu à l’observation d’étonnantes arabesques, telles que celles illustrées ci-dessous. Ce mouvement n’est cependant qu’apparent : il résulte du pivotement apparent du Soleil vu depuis un lieu donné dans son mouvement journalier dans le ciel. En réalité, c’est notre horizon local qui pivote et engendre la déformation de la trajectoire rectiligne de Mercure devant le Soleil.
devant le SoleilCrédits Y. Gominet/IMCCE
vue depuis ParisCrédits Y. Gominet/IMCCE
vue depuis Fort‑de‑FranceCrédits Y. Gominet/IMCCE
vue depuis Saint‑Denis (La Réunion)Crédits Y. Gominet/IMCCE
Calcul des circonstances locales
La visibilité du passage de Mercure devant le Soleil dépend du lieu depuis lequel le phénomène est observé. Le formulaire ci-dessous vous donne la possibilité de calculer les circonstances locales, c’est-à-dire de déterminer les instants des différents contacts extérieurs et intérieurs, la position angulaire de Mercure à ces instants vis-à-vis de la direction du pôle Nord céleste ou de la direction du zénith, ainsi que la position du Soleil dans le ciel.
Le lieu d’observation peut être déterminé interactivement en cliquant sur la carte ci-dessous ou au moyen du formulaire de saisie des coordonnées de longitude et de latitude.
Pour chaque contact, l’instant est calculé en Temps universel coordonné (UTC). Le maximum du passage correspond à l’instant où la distance entre le centre de Mercure et celui du Soleil est minimale, c’est donc le milieu du phénomène.
L’angle au pôle (P) représente la position angulaire de Mercure sur le disque du Soleil comptée positivement en tournant vers l’est à partir du pôle Nord céleste. L’angle au zénith (Z) représente la position angulaire de Mercure sur le disque du Soleil comptée positivement en tournant vers l’est à partir de la direction du zénith local. Ces angles permettent de connaître précisément les points d’entrée et de sortie de Mercure sur le disque solaire, soit dans un repère équatorial (angle au pôle), soit dans un repère local (angle au zénith).
Les données relatives à la visibilité du Soleil – et donc du phénomène – sont également affichées : la hauteur du Soleil donne sa position au-dessus de l’horizon local, tandis que l’azimut du Soleil donne sa position dans un plan horizontal, comptée positivement en tournant vers l’ouest à partir de la direction sud. Le passage au méridien local du Soleil se fait toujours à un azimut de 0° (ou de 360°). La hauteur du Soleil ne tient pas compte de la réfraction atmosphérique. Un contact est classé non visible si la hauteur du centre du Soleil à l’instant du contact est inférieure à − 36,6′.
| Instant | P | Z | Hsol | Azsol | ||
|---|---|---|---|---|---|---|
| h : min : s (UTC) | ° | ° | ° | ° | ||
Le calcul des circonstances locales de visibilité du passage de Mercure est effectué à l’aide des théories planétaires INPOP06 élaborées à l’IMCCE. Les précisions des positions des planètes intérieures dans ces théories est de l’ordre de 0,005 seconde de degré. L’obtention des coordonnées apparentes des astres nécessite l’usage de théories de la précession et de la nutation et du temps sidéral. Nous avons utilisé la théorie de la précession UAI 2000, la théorie de la nutation 2000A (2003) et le temps sidéral UAI 2000.
Ces prédictions dépendent également d’un certain nombre de paramètres physiques qui doivent être cohérents entre eux et avec les théories planétaires utilisées. Comme les théories INPOP06 utilisent la valeur de l’unité astronomique de l’IERS 1992 (a = 149 597 870,691 km), nous avons également utilisé les constantes IERS 1992 pour le demi-diamètre équatorial terrestre (R = 6 378,1363 km) et pour la valeur de la parallaxe équatoriale horizontale moyenne du Soleil (π0 = 8,794 143″ = arcsin(R/a)). Nous avons pris pour le demi-diamètre solaire à une unité astronomique (d = 15′59,63″) et pour le demi-diamètre de Mercure (d′ = 2 439,7 km). L’aplatissement terrestre est pris égal à 1/298,257 (IERS 1992).
L’échelle de temps utilisée dans les prédictions des temps de contact est le Temps universel coordonné (UTC ou UT), l’écart entre le Temps terrestre (TT) et le Temps universel UTC (TT−UTC) a été pris égal à 69,184 s. Le calcul des circonstances locales est mené à partir des éléments de Bessel, comme pour une éclipse solaire. L’écart interne avec un calcul direct utilisant les coordonnées topocentriques des deux astres est de l’ordre de quelques millièmes de seconde de temps.
Calcul de la parallaxe solaire
La parallaxe solaire est l’angle π☉ sous lequel le rayon équatorial terrestre est vu depuis le centre du Soleil. Cet angle est très petit, sa valeur est actuellement de 8,794 142 873″. Il est égal au rapport du rayon équatorial de la Terre par la distance Terre-Soleil. Cette distance est appelée « unité astronomique » et sa valeur exacte a été fixée à 149 597 870 700 mètres lors de l’assemblée générale de l’Union astronomique internationale en 2009.
Les instants de contact diffèrent d’un lieu à l’autre de la Terre en raison de l’effet de parallaxe qui résulte de la proximité relative de Mercure. C’est précisément l’observation de ces points de contact qui permet de mesurer la parallaxe et d’en déduire la distance entre le point d’observation et le Soleil.
Cette méthode de détermination de la parallaxe solaire a été utilisée lors des xviiie et xixe siècles à l’aide des passages de Vénus devant le Soleil et non à l’aide des passages de Mercure. Elle peut également être appliquée dans le cas de Mercure, en nécessitant toutefois une précision de mesure d’au moins 1 seconde de temps sur les différents instants des contacts, ce qui donne une incertitude d’environ 1% sur la parallaxe déduite, soit 0,09″ ou 1,5 million de kilomètres.
Dans le formulaire suivant, il vous suffit de saisir les valeurs des instants de contact que vous aurez pu mesurer et de valider à l’aide du bouton « Calculer ».
| π☉ | au | |
|---|---|---|
| ″ | km | |
Ressources pédagogiques
Vous trouverez ici différents supports pédagogiques pour approfondir certaines questions que soulèvent un événement tel que le passage de Mercure devant le Soleil, sur le passage lui-même ou sur l’astronomie en général.
6 posters
- La planète Mercure en 10 questions A3 4 × A3
- Les conditions du passage de Mercure A3 4 × A3
- L’observation du passage de Mercure A3 4 × A3
- La mission d’exploration de Mercure BepiColombo A3 4 × A3
- Les objectifs de la mission BepiColombo – 1re partie A3 4 × A3
- Les objectifs de la mission BepiColombo – 2e partie A3 4 × A3
Plusieurs fiches thématiques
- Observer le passage de Mercure au Solarscope A4
- La durée du jour sur Mercure A4
- Le champ magnétique de Mercure A4
- Les distances dans l’Univers A4
- Les planètes du Système solaire A4
- L’origine du nom des jours A4
- L’ordre des jours de la semaine A4
- La zone d’habitabilité A4
- Planétaire à monter A4
Autres ressources
- Mystérieuse Mercure : histoire illustrée pour les primaires A4
- Mercure et les astronomes : initiation à l’histoire des sciences pour le collège A4
Photographies du passage de Mercure devant le Soleil du 9 mai 2016 réalisées par l’IMCCE




Toutes ces ressources sont sous licence CC BY-NC-ND 4.0.